費用を固定費と変動費に分解することを固変分解という。固変分解の方法は演繹的な方法と帰納的な方法に大別できる。

演繹的な方法は、IE法（Industrial Engineering Method）と呼ばれる方法だ。これは、費用の動きを表す関数のようなものを論理的に見出す方法だ。しかし、そのような関数を見出すのは容易ではないので、あまり現実的な方法ではない。利用するとしても、限られたケースにしか利用できないのが普通だ。

帰納的な方法は、過去の実績から類推して固変分解する方法だ。その基本的な考え方は以下の通りだ。まず、売上高と費用の実績値をプロットし、何らかの方法でその近似直線を引く（下図）。この近似直線が縦軸と交わる点（いわゆる「y切片」）は、売上高が0のときでも存在する費用なので、これが固定費である。一方、近似直線の傾きは、売上高の変化に対する費用の変化なので、これが変動費率である。

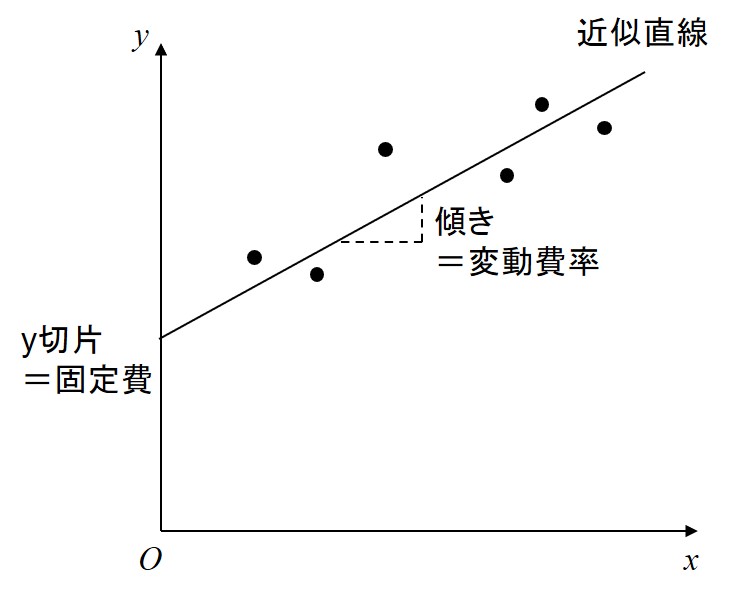
近似直線を引く代表的な“何らかの方法”は4つある。

1つ目は、費目別精査法（または勘定科目法）だ。この方法は、勘定科目毎に固定費か変動費かを決め打ちしてしまう方法だ。簡便なため、実務上最も多用されるが、決め打ちしてしまうために正確性に欠ける面がある。

2つ目は高低点法だ。これは、過去の実績データのうち、横軸方向の最高の点と最低の点を選び、その2点を結ぶ直線を総コスト線とみなす方法だ。計算量を少なくする効果はあるが、たった2点ですべてを推定することには無理がある。多くのデータを簡単に処理できる現在においては、実務上利用されることはほとんどないと言っていい。

3つ目はスキャッター・チャート法だ。これは目測で近似直線を外挿する方法だ。直線が一意に決まらない上に、再現性にも欠けるため、これも実務上はほとんど使われない。

4つ目の方法は最小自乗法だ。これは数学的に近似直線を求める方法だ。最も論理的な方法だが、費用の総額を機械的に固変分解してしまうので、どの費用が変動費または固定費なのかという紐付けができないというデメリットもある。

結局、実務に耐え得るのは費目別精査法か最小自乗法のいずれかである。